Visualising mental images to support calculation
May, 2021
One of the themes that has come up repeatedly in discussions we have had with teachers through this year is the power of children being able to ‘pull up’ mental images of numbers into their mind and manipulate them. We’re going to use this blog to show how the programme supports this, and how you can prompt and support children to do this.
In the last blog we talked about how to prompt children to move to independent strategy selection, and I gave the example of varying levels of prompting for 9 -7, which is covered by the Number Neighbours strategy. For some of the strategies though, I find one of the common prompts I use is asking children to close their eyes and visualise a mental image that we have looked at and discussed in class and then manipulate this. I’ll give a couple of examples of this.
Using visualisation to support calculation
9 – 6 is one of the subtraction facts that our conferencing shows children are most likely to count on their fingers to solve. We use the 9 square as an image to support children to calculate 9 – 6 and 9 – 3, as well as 3 + 6 and 6 + 3. In the programme children work through the stage of familiarising children with the 9 square image (Stage 1), then drawing attention to the 6 and 3 within it (Stage 2), and finally linking this to the associated calculations (Stage 3). If a child asked me what 9 – 6 was I would encourage them to visualise a mental image of 9, and manipulate this. “9 – 6. OK, close your eyes and think of your 9 square. Can you see it? OK, now can you imagine splitting off 6. Yes? What is the other part?” That is normally plenty of prompt for children to be able to calculate that it is 3, having worked through the gradual approach shown here.
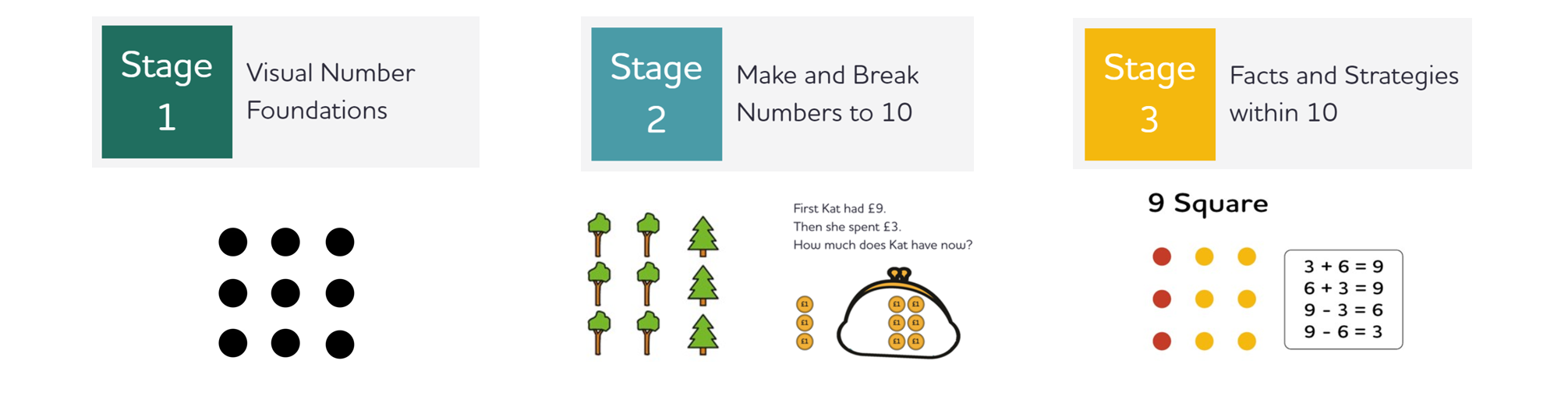
Another strategy that I find visualising incredibly powerful for is for children to start independently bridging through 10, which in Number Sense Maths is covered at the start of Stage 5 by the ‘Make 10 and Then’ strategy. For this we use the tens frame image. While it is important that children have plenty of opportunity to work physically with tens frames themselves, we do find the animations seem to have a certain power in helping build visual images of their own that they can 'call up' and then mentally manipulate as a route to independent strategy use. Here’s how I use them.
1. First of all, supported by the animation of adding (or subtracting) through ten using the tens frame image, discuss the structures that underpin the strategy: for example, for 8 + 5, first I add 2 to make 10, and then I add the other 3. Thirteen. The animations expose this with the movement of 2 counters from the second addend (5) to the first addend (8).
Once the children have understood the strategy, then play the animations again, just with children watching – no talk now. This seems to me to support a kind of 'laying down' of these visual images for children.
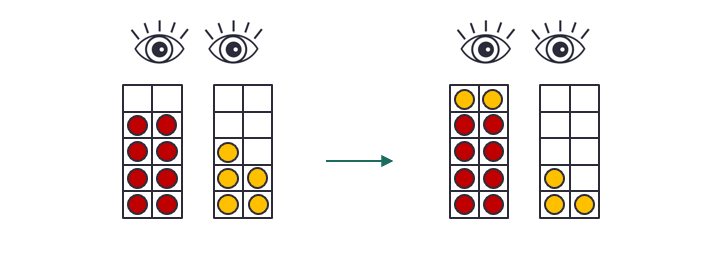
2. Next start pausing the animation once the starting image of the two addends appears. Now ask the children to visualise the addition from this static image. You’ll see the children starting to put fingers out as they ‘move’ counters from the second addend to the first. Encourage this – gesture is good! Use mini whiteboards to check children’s answers and who is getting this. Once they’ve imagined this, press play and let them watch it. “Was this what you saw in your head?”
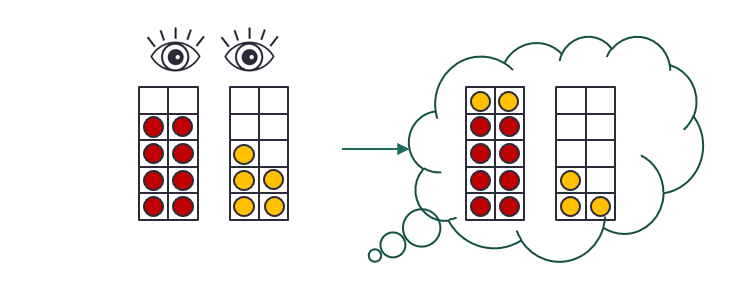
3. Finally ask children to close their eyes before the starting image of the two addends appears. So at this stage I would say “OK, now it is 9 + 4. Can you imagine that? 9 on that first ten frame. Think about how many gaps you have. Now 4 on the second ten frame. Try to get it in your head.” At this stage I also suggest that, if children want to, then can quickly open their eyes and ‘check’ their mental image with the one on the class whiteboard. I find it helpful to talk about ‘taking a quick picture’ and closing their eyes again. This provides an extra level of support for those who can’t initially bring those tens frames images up from scratch AND then manipulate them.
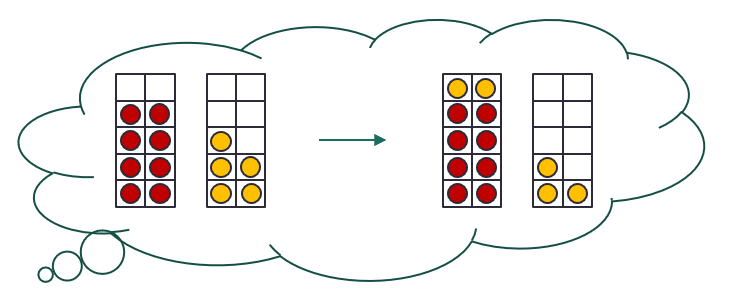
For the vast majority of children, this is enough to get them independently visualising the structure of bridging through 10. Like anything, the more they practice, the more confident they will get. For a very small minority of children I’ve found a couple of additional steps helpful. After the middle step, show them the two tens frames, but just with the first addend (here 8) actually shown. Ask them to look at it and imagine the second addend. Again, you’ll see those fingers out, placing the imaginary counters in the air. And then I’ve found just showing two empty tens frames is a further useful step, supporting the visualisation of both addends before they start working with closed eyes and imagining all of it (the final step above).
Although we wrote the programme and approach for Key Stage 1, bridging through 10 definitely needs consolidating through the first part of Year 3 (and for children who haven’t had systematic number fact teaching historically, at any stage of Key Stage 2). We've heard repeatedly from schools this year who have seen a dramatic difference in Year 3 children’s ability to bridge through 10 after a two week daily focus on this, supported by the animations. If you aren’t using the full programme yet, the Make 10 and Then addition animations are all freely available for you to have a go.
Supporting children to develop mental images
Of course, children need practice to be able to pull up and manipulate visual images in this way, and Stages 1 and 2 of the programme are all about attuning children to quantity and starting to build up mental images of numbers, before we actually start teaching the calculation strategies in Stage 3. Stage 1 introduces both the 9 square, and then tens frame, as well as some a couple of others structured arrangements that are drawn on in the course of the programme. The pupil conferencing assessment at the end of Stage 1 an easy way to check that children can recognise these.
Then Stage 2 provides children with experience of conceptual subitising – seeing both a whole quantity, and parts within it, and the idea of starting to mentally manipulate visual models. Each Stage 2 book starts with dot arrangements; the ones we provide for 9 are shown here, but you can of course make your own. Children love talking about these - all the different quantities they can see within a larger quantity, and we always say that, providing the children are saying what they see, there are no wrong answers! Don't try to lead the children towards particular number pairs. This is ALL about attuning children to quantity. Some may see 9 broken down into 9 ones, some may see ways of breaking up a quantity that the arrangement naturally leads you to, and some may see completely unexpected things. All are equally valid. A teacher last week told us that one of her children had seen the 9 square broken down into a 4 square, with 5 'wrapped around' the outside. This made me think of a lesson I've taught in upper Key Stage 2 working towards a generalisation about the difference between adjacent square numbers, which relies entirely on seeing square numbers composed in this way. As another of the teachers in that group session said, "The early mathematical toolkit in all its glory".

And then the everyday context animations, also within Stage 2, provide a gentle introduction to 'imagining'. Take this sandcastles image, from Make and Break 10 (there are similar animations for every other number to 10). We suggest that you pause the animation and look at the 10 sandcastles first. Can we imagine 3 of them being washed away? See it now in your head! Which 3 did you imagine being washed away? Come up to the board and show us! Who had the same picture as that in their head? Did anyone have a different picture in their head and imagine a different 3 being washed away? Playing the rest of the animation will provide a prompt for those struggling, but we find that when we start encouraging children to think in this way they really love it and the vast majority find it intuitive.

Children's earliest experiences with number involve a visual processing of small quantities. We come into the world primed and ready to subitise, but it is a skill that also needs nurturing. We've thought carefully in every element of the number fact progression we use about how we can meet children at their starting points, and build on this skill as a route to fluent calculation. For us, visualising has shown itself to play an important role in making fluency in number facts an achievable goal for all children, and an engaging and talk rich part of the process of getting there.
